Unsupervised learning: dimensionality reduction
Contents
Note
This lecture is going to:
Clarify the difference between supervised and unsupervised models
Show how we can visualize many features to get an idea of the distributions
Discuss how and why features may be correlated and how to measure the correlation
Introduce the concept of dimensionality reduction
using a linear method (PCA)
using a nonlinear method (tSNE)
Unsupervised learning: dimensionality reduction#
Let’s remind ourselves what supervised and unsupervised means in the context of machine learning:
supervised: We are building models that have some input data/features and some known output target/label (a number if regression, a categorical variable if classification)
unsupervised: We want models that only use the input data/features.
Since we’re often trying to predict something in engineering we’ve focused on supervised techniques so far. However, unsupervised learning is very helpful. The two most common use cases are:
dimensionality reduction: We want to reduce the number of input features
clustering: We want to cluster some data to find similar points in a dataset or understand the data distribution
We’re going to talk about dimensionality reduction today!
Dataset: Dow process impurity#
We’re going to use the Dow process dataset that you saw on your homework already.
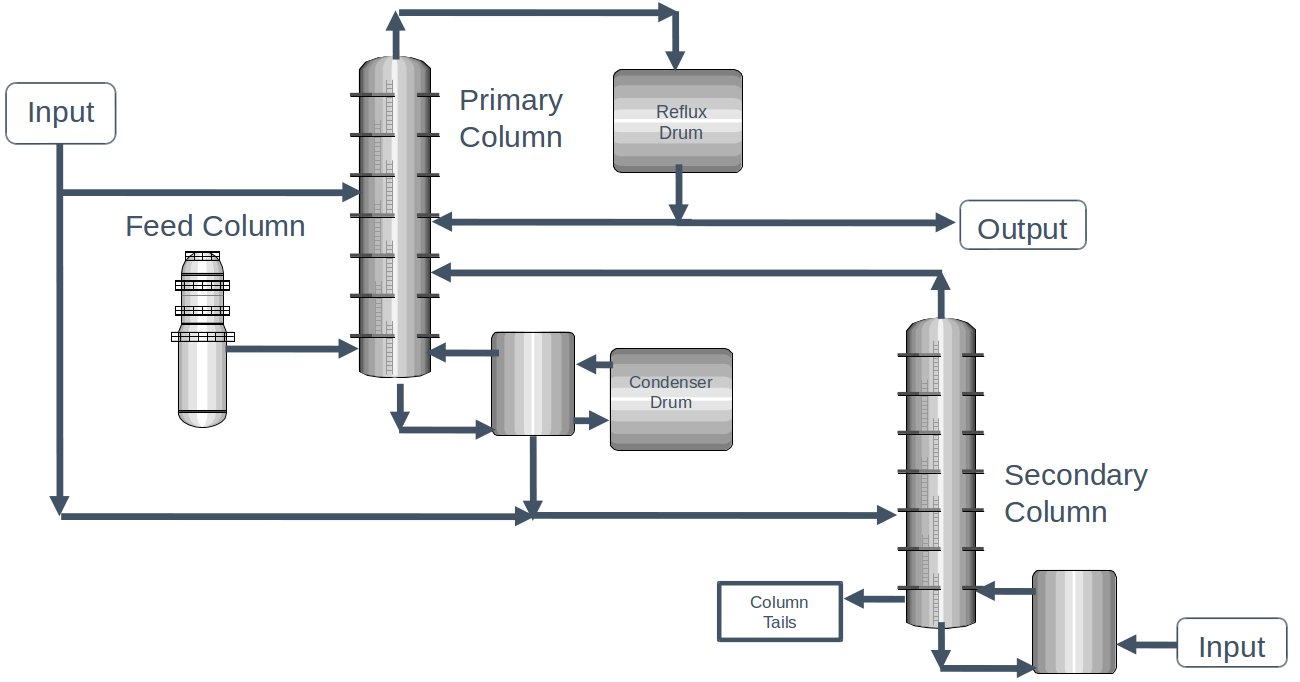
The dataset contains a number of operating conditions for each of the units in the process, as well as the concentration of impurities in the output stream. We’ll use the same filtering that you used on your homework to remove some problematic data points.
import numpy as np
import pandas as pd
df = pd.read_excel("datasets/impurity_dataset-training.xlsx")
def is_real_and_finite(x):
if not np.isreal(x):
return False
elif not np.isfinite(x):
return False
else:
return True
all_data = df[df.columns[1:]].values # drop the first column (date)
numeric_map = df[df.columns[1:]].applymap(is_real_and_finite)
real_rows = (
numeric_map.all(axis=1).copy().values
) # True if all values in a row are real numbers
X = np.array(
all_data[real_rows, :-5], dtype="float"
) # drop the last 5 cols that are not inputs
y = np.array(all_data[real_rows, -3], dtype="float")
x_names = [str(x) for x in df.columns[1:41]]
y_name = str(df.columns[-3])
Let’s remind ourselves how big this dataset is (# of points and # of features)
print(f"There are {X.shape[0]} data points in the impurity dataset")
print(f"There are {X.shape[1]} features in the impurity dataset")
There are 10297 data points in the impurity dataset
There are 40 features in the impurity dataset
Let’s also make a simple 80/20 train/test split. This is important since some of the data analysis techniques will be used to build better supervised models.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, train_size=0.8, random_state=42
)
One of the challenges with data with 40 dimensions is that it’s extremely hard to visualize. 2-3 dimensions is pretty straightforward, but 40 is impossible!
Visualization of features#
Unlike working with a single variable where we can plot “x vs. y”, but it is difficult to get a feel for higher-dimension data since it is hard to visualize. One good thing to start with is looking at histograms of each input variable. This is super easy using dataframes!
df[df.columns[1:41]].hist(bins=30, figsize=(30, 20));
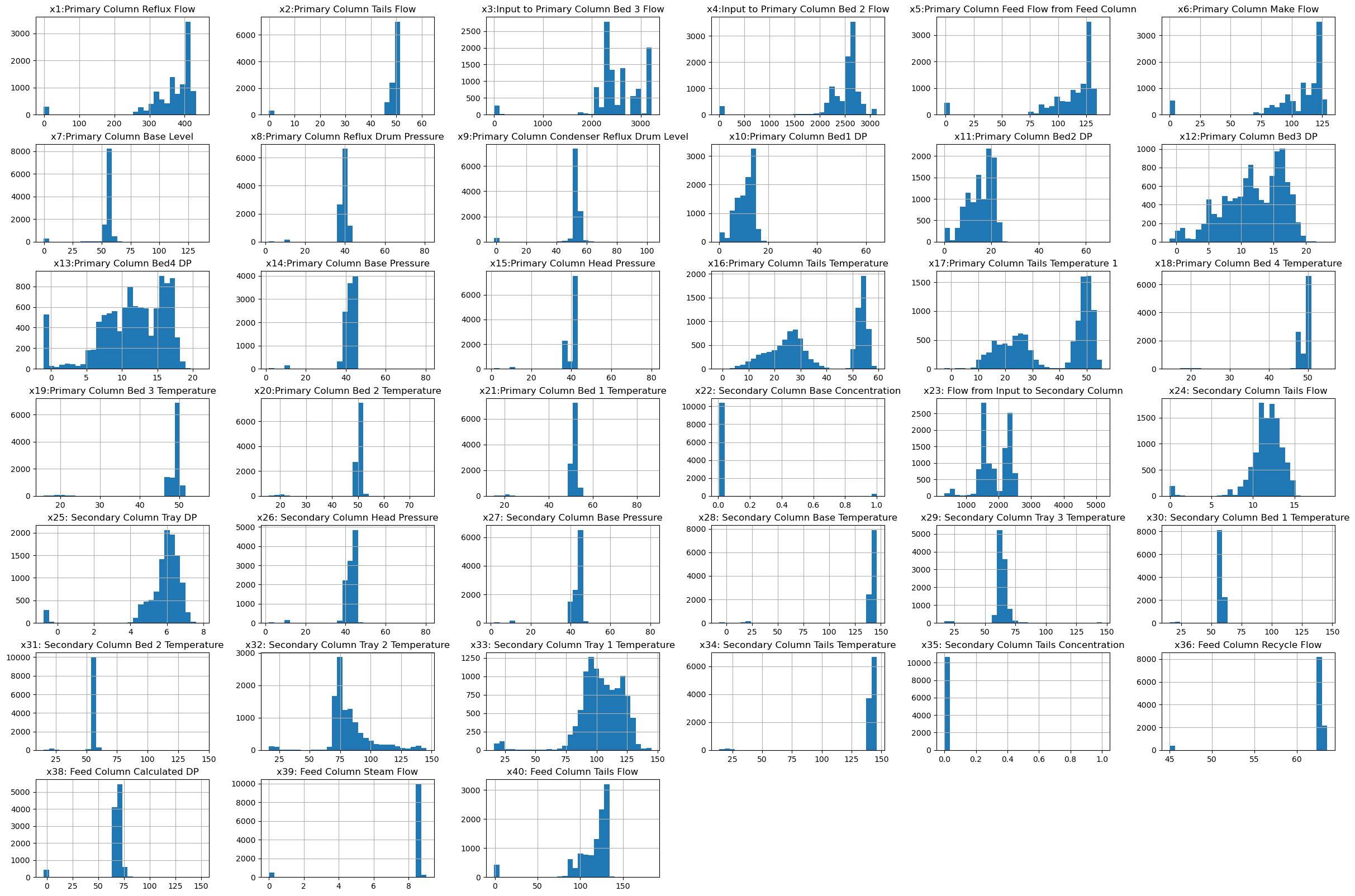
We can see that some features are normally distributed, while others have some obvious outliers or bimodal distribution. We have no idea how these features are correlated yet - that is if any of them are related.
Feature correlations#
There are 40 features in the dataset, but from our engineering knowledge we expect that some might end up being correlated. For example, if there’s an energy balance, the energy in one unit may be directly correlated with the energy in another unit or stream.
Practice#
Before we try this numerically, let’s take a look at the features and the diagram and see if we can come up with any guesses as to some variables that might be correlated.
x_names
['x1:Primary Column Reflux Flow',
'x2:Primary Column Tails Flow',
'x3:Input to Primary Column Bed 3 Flow',
'x4:Input to Primary Column Bed 2 Flow',
'x5:Primary Column Feed Flow from Feed Column',
'x6:Primary Column Make Flow',
'x7:Primary Column Base Level',
'x8:Primary Column Reflux Drum Pressure',
'x9:Primary Column Condenser Reflux Drum Level',
'x10:Primary Column Bed1 DP',
'x11:Primary Column Bed2 DP',
'x12:Primary Column Bed3 DP',
'x13:Primary Column Bed4 DP',
'x14:Primary Column Base Pressure',
'x15:Primary Column Head Pressure',
'x16:Primary Column Tails Temperature',
'x17:Primary Column Tails Temperature 1',
'x18:Primary Column Bed 4 Temperature',
'x19:Primary Column Bed 3 Temperature',
'x20:Primary Column Bed 2 Temperature',
'x21:Primary Column Bed 1 Temperature',
'x22: Secondary Column Base Concentration',
'x23: Flow from Input to Secondary Column',
'x24: Secondary Column Tails Flow',
'x25: Secondary Column Tray DP',
'x26: Secondary Column Head Pressure',
'x27: Secondary Column Base Pressure',
'x28: Secondary Column Base Temperature',
'x29: Secondary Column Tray 3 Temperature',
'x30: Secondary Column Bed 1 Temperature',
'x31: Secondary Column Bed 2 Temperature',
'x32: Secondary Column Tray 2 Temperature',
'x33: Secondary Column Tray 1 Temperature',
'x34: Secondary Column Tails Temperature',
'x35: Secondary Column Tails Concentration',
'x36: Feed Column Recycle Flow',
'x37: Feed Column Tails Flow to Primary Column',
'x38: Feed Column Calculated DP',
'x39: Feed Column Steam Flow',
'x40: Feed Column Tails Flow']
Correlation coefficient#
We can formalize this concept with a correlation coefficient. The most common/useful correlation coefficient is the Pearson correlation coefficient. It is a number in the range [-1,1] that describes how correlated two variables are. I find this plot from the wikipedia page to be extremely helpful!
See also
https://en.wikipedia.org/wiki/Pearson_correlation_coefficient
Now, Let’s try this for our data! df.corr() calculates the correlation coefficient for all columns in the dataset
import plotly.express as px
import plotly.graph_objects as go
import plotly.io as pio
# Found this snippet by googling "correlation matrix plotly"
# and finding https://stackoverflow.com/questions/66572672/correlation-heatmap-in-plotly
pio.templates.default = "plotly_white"
fig = go.Figure()
fig.add_heatmap(
z=df[df.columns[1:41]].corr(),
x=x_names,
y=x_names,
colorscale=px.colors.diverging.RdBu,
zmin=-1,
zmax=1,
)
fig.update_layout(autosize=False, width=800, height=800)
fig.show()
/tmp/ipykernel_1322/3546208615.py:12: FutureWarning:
The default value of numeric_only in DataFrame.corr is deprecated. In a future version, it will default to False. Select only valid columns or specify the value of numeric_only to silence this warning.
This plot has some very interesting structure!
The diagonal is 1 - every feature is perfectly correlated with itself
The plot is symmetric - the correlation between x1 and x2 is the same as the correlation between x2 and x1
Many pairs have a strong positive (~1) correlation
Some pairs have a very weak correlation
A few pairs have strong negative correlation
There are some obvious groups among the features. For example, all of the primary column bed temperatures are strongly correlated with each other.
Let’s plot a few of these just to see what happens.
Example of positive correlation#
import plotly.express as px
import plotly.graph_objects as go
import plotly.io as pio
fig = go.Figure()
fig.add_scatter(
x=df["x18:Primary Column Bed 4 Temperature"],
y=df["x19:Primary Column Bed 3 Temperature"],
mode="markers",
)
fig.update_layout(autosize=False, width=600, height=600)
fig.update_xaxes(title_text="x18:Primary Column Bed 4 Temperature")
fig.update_yaxes(title_text="x19:Primary Column Bed 3 Temperature")
fig.show()
It’s probably not so surprising that the temperature in beds next to each other in the same column are pretty strongly correlated!
Interestingly there are a few strong outliers here - that could either be noise or erroneous datapoints, or could be really interesting and rare scenarios. We don’t really know unless we dig into the actual data. I would probably select a few of those conditions and investigate what happened at those specific times!
Example of negative correlation#
Let’s try one of the negative ones from the matrix above
import plotly.express as px
import plotly.graph_objects as go
import plotly.io as pio
fig = go.Figure()
fig.add_scatter(
x=df["x34: Secondary Column Tails Temperature"],
y=df["x22: Secondary Column Base Concentration"],
mode="markers",
)
fig.update_layout(autosize=False, width=600, height=600)
fig.update_xaxes(title_text="x34: Secondary Column Tails Temperature")
fig.update_yaxes(title_text="x22: Secondary Column Base Concentration")
fig.show()
This one is a little less clear - there’s clearly a correlated. All of the points with high tails temperature in the second column also have a very low base concentration. I can’t explain this without thinking a little more about the chemical engineering process, but it immediately jumps out from the data.
Be careful though - correlation is not causation!
Dimensionality reduction#
We can take advantage of the fact that many of the features are correlated to reduce the number of features in our system. From the example above, we probably don’t need all of the temperatures in the beds of the first column, unless those outliers happen to be important!
Many dimensionality reduction techniques are implemented in scikit-learn. We’ll try just two simple ones here.
Practical uses of dimensionality reduction#
There are a number of practical uses for dimensionality reduction algorithms:
compression of data
denoising of data
interpretation of data
improving model efficiency or performance
We will focus primarily on the ways that dimensionality reduction can aid in interpretation and improving model efficiency and performance, but the algorithms used for other applications are the same or similar.
Considerations for dimensionality reduction#
There are many different kinds of dimensionality reduction approaches, and when selecting between them there are a few things to consider. The relative importance of these factors will depend on the nature of the dataset and the goal of the analysis.
Matrix rank - how many independent dimensions are there?
Linearity of the low-dimensional subspace - are patterns linear or non-linear?
Projection - can a new high-dimensional point be projected onto the low-dimensional map?
Inversion - can a new low-dimensional point be projected back into high-dimensional space?
Supervised vs. unsupervised - are the training labels used to determine the reduced dimensions?
Assessing performance of dimensionality reduction models#
It can be challenging to assess the performance of dimensional reduction models, especially when unsupervised. Nonetheless there are a few approaches that can be used. Selecting the right approach will depend on the problem, but using a variety of assessment criteria is always a good idea if possible.
Explained Variance (most common)#
One common idea in dimensional reduction is to assess the “explained variance” of the high-dimensional data. This is common in techniques such as PCA.
Distance#
The “stress” function compares the distance between points \(i\) and \(j\) in a low-dimensional space to the distance in the full-dimensional space:
\( S(\vec{x}_{0}, \vec{x}_1, \vec{x}_2, ... \vec{x}_n) = \left( \frac{\sum_{i=0}^n \sum_{i<j}(d_{ij} - ||x_i - x_j||)^2}{\sum_{i=0}^n \sum_{i<j} d_{ij}^2} \right)^{1/2} \)
where \(d_{ij}\) is the distance in the high-dimensional space and \(\vec{x}\) is the vector in the low-dimensional space.
A conceptually similar way to express this is:
\(\sum_i \sum_j || d(\vec{x}_i, \vec{x}_j) - d(P(\vec{x}_i), P(\vec{x}_j))||\)
where \(d(\vec{x}_i, \vec{x}_j)\) is the distance between \(\vec{x}_i\) and \(\vec{x}_j\) in the high-dimensional space, and \(P(\vec{x}_j)\) is the reduced-dimension vector.
Some approaches seek to minimize these distances directly (e.g. multi-dimensional scaling), but it can also be used as an accuracy metric. We can implement this using a few helper functions. You don’t need to worry about the details of this function, but can look up the documentation to see the connection.
Principal component analysis#
You can identify linear combinations of the original features that contain independent information using principal component analysis (PCA). PCA works by using the eigenvectors of the covariance matrix to identify linear combinations. The eigenvectors of the covariance matrix identify the “natural” coordinate system of the data.
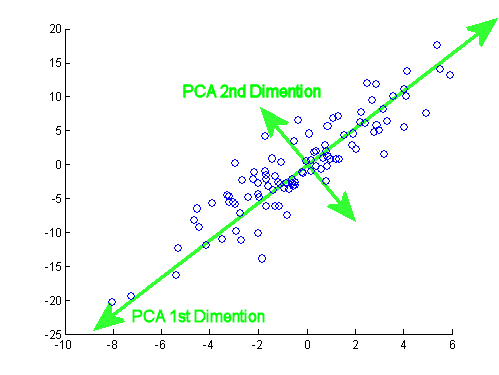
PCA isn’t too hard to implement from scratch, but we’ll use the sklearn interface since the details are not so important. Unsupervised methods like PCA have a similar interface to sklearn ML models, but instead of a predict function they have a transform function.
See also
sklearn PCA: https://scikit-learn.org/stable/modules/decomposition.html#pca
scatter matrix: https://plotly.com/python/splom/
import plotly.express as px
from sklearn.decomposition import PCA
# Default PCA object
pca = PCA()
# Fit the PCA and transform the data
components = pca.fit_transform(X_train)
# Get the explained variance from the PCA object
# and format it as a string
labels = {
str(i): f"PC {i+1} ({var:.1f}%)"
for i, var in enumerate(pca.explained_variance_ratio_ * 100)
}
# Plot with plotly!
fig = px.scatter_matrix(
components,
labels=labels,
hover_data={
a: b for a, b in zip(x_names, X_train.T)
}, # add the rest of the data on hover!
dimensions=range(4),
)
fig.update_traces(diagonal_visible=False)
fig.update_layout(autosize=False, width=800, height=800)
fig.show()
/opt/conda/lib/python3.9/site-packages/plotly/express/_core.py:279: FutureWarning:
iteritems is deprecated and will be removed in a future version. Use .items instead.
Notice that the first three principal components explain almost all of the data as most of the features are correlated. We could use these three components as features in a supervised ML model. You will try that in your homework!
t-SNE manifold learning#
t-SNE (t-distributed stochastic neighbor embedding) is another popular method for learning low-dimensional representation of high-dimensional data. t-SNE operates by trying to find a low-dimensional representation that minimizes the stress above. Effectively, you want to learn a manifold such that points that are close in the new space are also close in the high-dimensional space. It is particularly helpful for clustering high-dimensional data.
As the name implies, tSNE is stochastic, which means that the results you get will change each time you run it unless you set the seed.
Let’s see how it does! This code takes a while to run (~2min).
See also
tSNE in sklearn: https://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html
Original tSNE paper (2008): https://www.jmlr.org/papers/volume9/vandermaaten08a/vandermaaten08a.pdf
import plotly.express as px
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
# Default TSNE object
tsne = TSNE(init="pca", n_iter=1000, verbose=2)
# Fit the TSNE and transform the data
components = tsne.fit_transform(X_train)
/opt/conda/lib/python3.9/site-packages/sklearn/manifold/_t_sne.py:810: FutureWarning:
The default learning rate in TSNE will change from 200.0 to 'auto' in 1.2.
[t-SNE] Computing 91 nearest neighbors...
[t-SNE] Indexed 8237 samples in 0.000s...
[t-SNE] Computed neighbors for 8237 samples in 0.884s...
[t-SNE] Computed conditional probabilities for sample 1000 / 8237
[t-SNE] Computed conditional probabilities for sample 2000 / 8237
[t-SNE] Computed conditional probabilities for sample 3000 / 8237
[t-SNE] Computed conditional probabilities for sample 4000 / 8237
[t-SNE] Computed conditional probabilities for sample 5000 / 8237
[t-SNE] Computed conditional probabilities for sample 6000 / 8237
[t-SNE] Computed conditional probabilities for sample 7000 / 8237
[t-SNE] Computed conditional probabilities for sample 8000 / 8237
[t-SNE] Computed conditional probabilities for sample 8237 / 8237
[t-SNE] Mean sigma: 16.627640
[t-SNE] Computed conditional probabilities in 0.418s
/opt/conda/lib/python3.9/site-packages/sklearn/manifold/_t_sne.py:996: FutureWarning:
The PCA initialization in TSNE will change to have the standard deviation of PC1 equal to 1e-4 in 1.2. This will ensure better convergence.
[t-SNE] Iteration 50: error = 62.3327141, gradient norm = 0.0258344 (50 iterations in 5.604s)
[t-SNE] Iteration 100: error = 59.9432640, gradient norm = 0.0174837 (50 iterations in 5.354s)
[t-SNE] Iteration 150: error = 58.3277473, gradient norm = 0.0137707 (50 iterations in 5.066s)
[t-SNE] Iteration 200: error = 57.1936798, gradient norm = 0.0088780 (50 iterations in 4.862s)
[t-SNE] Iteration 250: error = 56.7727776, gradient norm = 0.0069002 (50 iterations in 4.798s)
[t-SNE] KL divergence after 250 iterations with early exaggeration: 56.772778
[t-SNE] Iteration 300: error = 1.2315521, gradient norm = 0.0008243 (50 iterations in 4.805s)
[t-SNE] Iteration 350: error = 1.1160257, gradient norm = 0.0003468 (50 iterations in 4.892s)
[t-SNE] Iteration 400: error = 1.0535544, gradient norm = 0.0002489 (50 iterations in 4.937s)
[t-SNE] Iteration 450: error = 1.0077178, gradient norm = 0.0002156 (50 iterations in 4.892s)
[t-SNE] Iteration 500: error = 0.9713467, gradient norm = 0.0001733 (50 iterations in 4.916s)
[t-SNE] Iteration 550: error = 0.9385639, gradient norm = 0.0001871 (50 iterations in 4.941s)
[t-SNE] Iteration 600: error = 0.9135734, gradient norm = 0.0001576 (50 iterations in 4.895s)
[t-SNE] Iteration 650: error = 0.8917339, gradient norm = 0.0001271 (50 iterations in 4.880s)
[t-SNE] Iteration 700: error = 0.8729308, gradient norm = 0.0001490 (50 iterations in 4.820s)
[t-SNE] Iteration 750: error = 0.8547539, gradient norm = 0.0001402 (50 iterations in 4.869s)
[t-SNE] Iteration 800: error = 0.8399104, gradient norm = 0.0001127 (50 iterations in 4.829s)
[t-SNE] Iteration 850: error = 0.8267508, gradient norm = 0.0001062 (50 iterations in 4.875s)
[t-SNE] Iteration 900: error = 0.8171217, gradient norm = 0.0001057 (50 iterations in 4.811s)
[t-SNE] Iteration 950: error = 0.8040411, gradient norm = 0.0001341 (50 iterations in 4.739s)
[t-SNE] Iteration 1000: error = 0.7956480, gradient norm = 0.0000963 (50 iterations in 4.792s)
[t-SNE] KL divergence after 1000 iterations: 0.795648
# Plot with plotly!
fig = px.scatter(
x=components[:, 0],
y=components[:, 1],
hover_data={
a: b for a, b in zip(x_names, X_train.T)
}, # add the rest of the data on hover!
color=y_train,
)
fig.update_layout(autosize=False, width=800, height=800)
fig.show()
We can see that there are some significant clusters that have emerged, and if you zoom in the larger clusters also have clusters. Probably this is coming from multiple data points collected near each other in time.
Other dimensionality reduction techniques#
There are many other methods that can be tried. sklearn has many of these implementations!
See also
https://scikit-learn.org/stable/modules/decomposition.html#principal-component-analysis-pca
https://scikit-learn.org/stable/modules/manifold.html
Isomap embedding#
As another example just to show all of these methods are different ways of doing the same thing, let’s try Isomap embeddings (https://scikit-learn.org/stable/modules/generated/sklearn.manifold.Isomap.html)
import plotly.express as px
from sklearn.decomposition import PCA
from sklearn.manifold import Isomap
# Default PCA object
isomap = Isomap()
# Fit the PCA and transform the data
components = isomap.fit_transform(X_train)
/opt/conda/lib/python3.9/site-packages/sklearn/manifold/_isomap.py:348: UserWarning:
The number of connected components of the neighbors graph is 11 > 1. Completing the graph to fit Isomap might be slow. Increase the number of neighbors to avoid this issue.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
/opt/conda/lib/python3.9/site-packages/scipy/sparse/_index.py:103: SparseEfficiencyWarning:
Changing the sparsity structure of a csr_matrix is expensive. lil_matrix is more efficient.
# Plot with plotly!
fig = px.scatter(
x=components[:, 0],
y=components[:, 1],
hover_data={
a: b for a, b in zip(x_names, X_train.T)
}, # add the rest of the data on hover!
color=y_train,
)
fig.update_layout(autosize=False, width=800, height=800)
fig.show()
Vote for next class lecture!#
Clustering (identifying groups of similar data)
Design of experiments / Bayesian Optimization (how to choose the best experiments to run to maximize or minimize something)



