Note

This lecture is going to:

Discuss the concept of parametric vs non-parametric models
Introduce a new dataset for spectra fitting problems that you might see if using analytical chemistry techniques
Summarize several of the most common non-parametric models

Non-parametric models#

Parametric models fit parameters within models to represent some underlying data. Everything we’ve done so far has been a parametric model. A few examples:

Linear regression
Polynomial regression (which is really linear regression with polynomial features)
Logistic regression
Non-linear regression (like we implemented with lmfit)
Neural networks
…

Non-parametric models don’t explicitly fit parameters, but use other approaches to predict data. A few examples, some of which we will cover today:

Decision trees
kernel regression
K-nearest neighbors (KNN)
Gaussian Processes
…

Parametric models tend to work best when you have a lot of data, and conversely non-parametric models tend to work better with small amounts of data. Some of this is because of differences in flexibility of the models, and part is because non-parametric models tend to get more computationally expensive with increasingly large datasets!

Because non-parametric models are not learning underlying patterns in the dataset, they also tend to have trouble extrapolating to data that is different from the training dataset.

Example dataset - IR spectra#

Let’s consider fitting models to experimental IR spectra. These models might be useful if you have an experimental measurement that is a bit noisy, or perhaps you want to predict the spectra in between data points.

import pandas as pd
import plotly.express as px

df = pd.read_csv("data/ethanol_IR.csv")

fig = px.line(df, x="wavenumber [cm^-1]", y="absorbance", title="Ethanol IR Spectra")
fig.update_xaxes(title_text="Wavenumber [cm^-1]")
fig.update_yaxes(title_text="Absorbence [AU]")
fig.show()

Before we jump in, a few interesting things about the dataset

Some of the absorbance values are negative (!!)
There’s a number of different peaks
It’s unclear if the noise is uniform everywhere (e.g. the IR spectra at lower wavenumbers looks more noisy than at higher wavenumbers)

Train/Val/Test split (given every 10th spectra, predict the rest)#

As always, let’s start with a train/val/test split. To make this interesting, let’s to 10/45/45 train/val/test. We’ll sample the training set uniformly, so that this is representative of a challenge where we have a low-quality IR spectra and want to predict a high-quality one.

That is, given one one tenth of the data, predict the rest.

from sklearn.model_selection import train_test_split

df_train = df[df.index % 10 == 0]
df_valtest = df[df.index % 10 != 0]
df_val, df_test = train_test_split(df_valtest, train_size=0.5, random_state=42)

import plotly.graph_objects as go

# Plot with plotly!
fig = go.Figure()
fig.add_scatter(
    x=df["wavenumber [cm^-1]"], y=df["absorbance"], name="Actual spectra data"
)
fig.add_scatter(
    x=df_train["wavenumber [cm^-1]"],
    y=df_train["absorbance"],
    name="Train data",
    mode="markers",
)
fig.add_scatter(
    x=df_val["wavenumber [cm^-1]"],
    y=df_val["absorbance"],
    name="Validation spectra",
    mode="markers",
)
fig.add_scatter(
    x=df_test["wavenumber [cm^-1]"],
    y=df_test["absorbance"],
    name="Test data",
    mode="markers",
)
fig.update_xaxes(title_text="Wavenumber [cm^-1]")
fig.update_yaxes(title_text="Absorbence [AU]")
fig.show()

(.686+.292+.016+.114+.019)/5

0.2254

K-Nearest Neighbors#

One of the strategies we discussed for predicting values of unseen data is to simply look at the nearest training data and average those predictions. This strategy is known as K-Nearest Neighbors (KNN). K is the number of neighbors that we want to average over.

This is very easy to implement in sklearn! Non-parametric models implement the same interface, and are required to have fit and predict functions.

from sklearn.metrics import mean_absolute_error, mean_squared_error
from sklearn.neighbors import KNeighborsRegressor

# Initialize and fit a KNN model
# n_neighbors here is the number of numbers to use in the prediction
model = KNeighborsRegressor(n_neighbors=5)

# KNN has a fit function like every other supervised method in sklearn
model.fit(
    X=df_train["wavenumber [cm^-1]"].values.reshape((-1, 1)),
    y=df_train["absorbance"].values.reshape((-1, 1)),
)

val_MAE = mean_absolute_error(
    df_val["absorbance"].values.reshape((-1, 1)),
    model.predict(df_val["wavenumber [cm^-1]"].values.reshape((-1, 1))),
)
print(f"The MAE for this KNN is {val_MAE:0.2f}")

The MAE for this KNN is 0.04

import numpy as np
import plotly.graph_objects as go

# Plot with plotly!
fig = go.Figure()
fig.add_scatter(
    x=df["wavenumber [cm^-1]"], y=df["absorbance"], name="Actual spectra data"
)
fig.add_scatter(
    x=df_train["wavenumber [cm^-1]"],
    y=df_train["absorbance"],
    name="Train data",
    mode="markers",
)
X_eval = np.arange(250, 4000, 0.1)
fig.add_scatter(
    x=X_eval,
    y=model.predict(X_eval.reshape((-1, 1))).reshape(
        (-1)
    ),  # Some tricks to make sure this is a vector
    name="K Neighbor Regression spectra",
    line_color="#ff0000",
)
fig.add_scatter(
    x=df_val["wavenumber [cm^-1]"],
    y=df_val["absorbance"],
    name="Validation spectra",
    mode="markers",
)
fig.update_xaxes(title_text="Wavenumber [cm^-1]")
fig.update_yaxes(title_text="Absorbence [AU]")
fig.show()

from sklearn.metrics import mean_absolute_error, mean_squared_error
from sklearn.neighbors import KNeighborsRegressor

# Initialize and fit a KNN model
# n_neighbors here is the number of numbers to use in the prediction
model = KNeighborsRegressor(n_neighbors=5,
                           weights='distance')

# KNN has a fit function like every other supervised method in sklearn
model.fit(
    X=df_train["wavenumber [cm^-1]"].values.reshape((-1, 1)),
    y=df_train["absorbance"].values.reshape((-1, 1)),
)

val_MAE = mean_absolute_error(
    df_val["absorbance"].values.reshape((-1, 1)),
    model.predict(df_val["wavenumber [cm^-1]"].values.reshape((-1, 1))),
)
print(f"The MAE for this KNN is {val_MAE:0.24f}")


import numpy as np
import plotly.graph_objects as go

# Plot with plotly!
fig = go.Figure()
fig.add_scatter(
    x=df["wavenumber [cm^-1]"], y=df["absorbance"], name="Actual spectra data"
)
fig.add_scatter(
    x=df_train["wavenumber [cm^-1]"],
    y=df_train["absorbance"],
    name="Train data",
    mode="markers",
)
X_eval = np.arange(250, 4000, 0.1)
fig.add_scatter(
    x=X_eval,
    y=model.predict(X_eval.reshape((-1, 1))).reshape(
        (-1)
    ),  # Some tricks to make sure this is a vector
    name="K Neighbor Regression spectra",
    line_color="#ff0000",
)
fig.add_scatter(
    x=df_val["wavenumber [cm^-1]"],
    y=df_val["absorbance"],
    name="Validation spectra",
    mode="markers",
)
fig.update_xaxes(title_text="Wavenumber [cm^-1]")
fig.update_yaxes(title_text="Absorbence [AU]")
fig.show()

The MAE for this KNN is 0.021971137168026611680149

Warning

Note that KNN with uniform weights yields a piecewise function with zero derivatives everywhere (except at the discontinuities). This could lead to very unhelpful optimization results if you’re trying to minimize or maximize the function/model!

Practice#

Try varying the number of neighbors and the weights parameter. How does this change the results? Can you get better validation results then above?

Decision Trees#

Decision trees are a non-parametric model that recursively splits the data. The general strategy is something like:

Start with all data in the same bin
Choose a random (or best) feature. Find the value of the feature that best separates the bin into two bins with large difference in mean values
Repeat for all bins until the bins are a minimum size or progress is not being made, or we hit a max depth (many possible choices here!) One really nice advantage of this process is that we can examine the learned rules to see how the model is making its decisions!

Let’s see this in practice using sklearn!

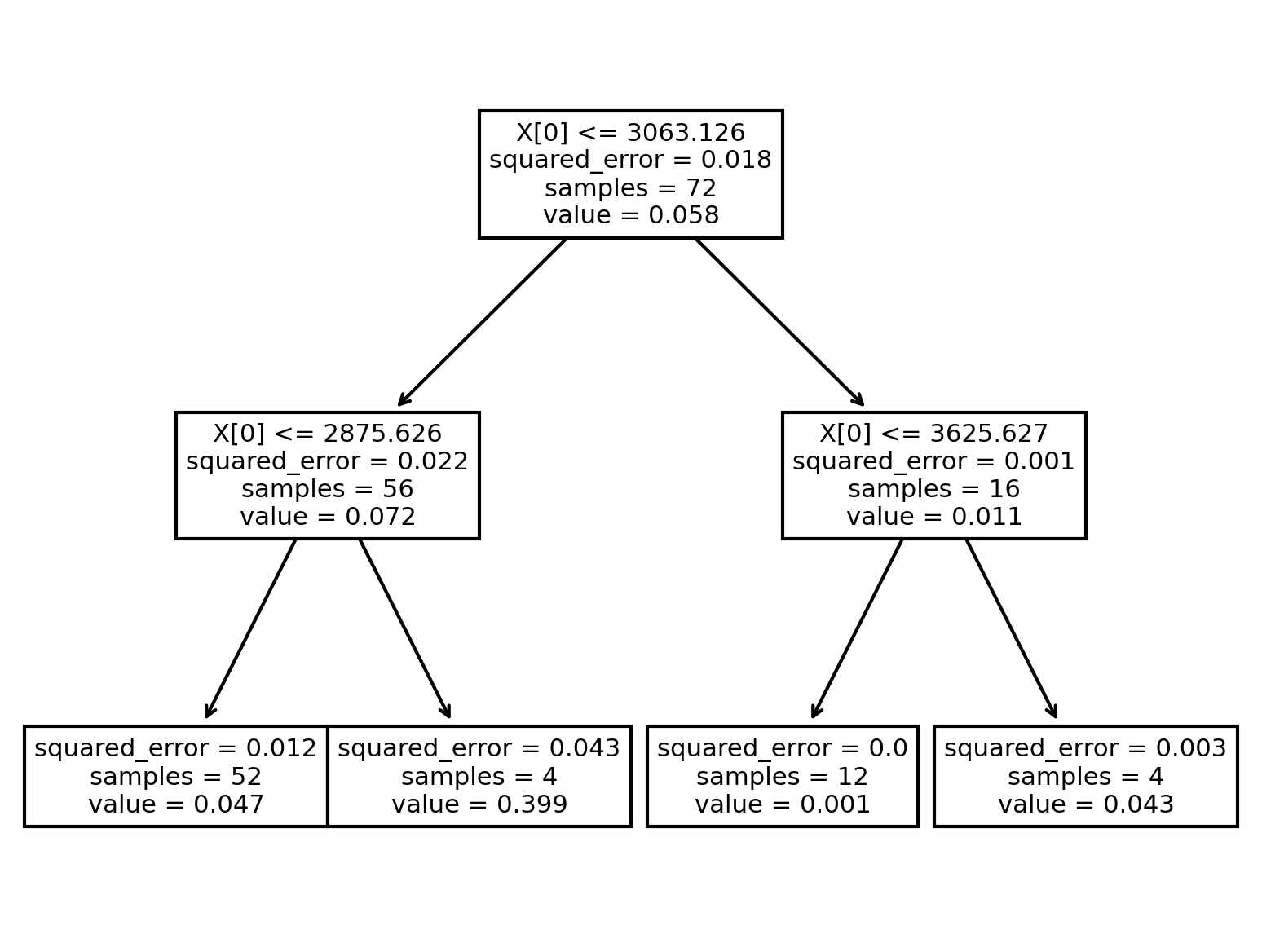
Visualizing decision trees#

We can visualize the decisions made in the model. To keep this easy to read we’ll limit the tree to a max depth of 2. If we had many possible features, these splits would also help us understand which features were most important.

import matplotlib.pyplot as plt
from sklearn import tree

model = DecisionTreeRegressor(max_depth=2)

# KNN has a fit function like every other supervised method in sklearn
model.fit(
    X=df_train["wavenumber [cm^-1]"].values.reshape((-1, 1)),
    y=df_train["absorbance"].values.reshape((-1, 1)),
)

plt.figure(dpi=300)
tree.plot_tree(model)

[Text(0.5, 0.8333333333333334, 'X[0] <= 3063.126\nsquared_error = 0.018\nsamples = 72\nvalue = 0.058'),
 Text(0.25, 0.5, 'X[0] <= 2875.626\nsquared_error = 0.022\nsamples = 56\nvalue = 0.072'),
 Text(0.125, 0.16666666666666666, 'squared_error = 0.012\nsamples = 52\nvalue = 0.047'),
 Text(0.375, 0.16666666666666666, 'squared_error = 0.043\nsamples = 4\nvalue = 0.399'),
 Text(0.75, 0.5, 'X[0] <= 3625.627\nsquared_error = 0.001\nsamples = 16\nvalue = 0.011'),
 Text(0.625, 0.16666666666666666, 'squared_error = 0.0\nsamples = 12\nvalue = 0.001'),
 Text(0.875, 0.16666666666666666, 'squared_error = 0.003\nsamples = 4\nvalue = 0.043')]

import numpy as np
import plotly.graph_objects as go

# Plot with plotly!
fig = go.Figure()
fig.add_scatter(
    x=df["wavenumber [cm^-1]"], y=df["absorbance"], name="Actual spectra data"
)
fig.add_scatter(
    x=df_train["wavenumber [cm^-1]"],
    y=df_train["absorbance"],
    name="Train data",
    mode="markers",
)
X_eval = np.arange(250, 4000, 0.1)
fig.add_scatter(
    x=X_eval,
    y=model.predict(X_eval.reshape((-1, 1))).reshape(
        (-1)
    ),  # Some tricks to make sure this is a vector
    name="Decision Tree Regressor spectra",
    line_color="#ff0000",
)
fig.add_scatter(
    x=df_val["wavenumber [cm^-1]"],
    y=df_val["absorbance"],
    name="Validation spectra",
    mode="markers",
)
fig.update_xaxes(title_text="Wavenumber [cm^-1]")
fig.update_yaxes(title_text="Absorbence [AU]")
fig.show()

Practice#

Try varying the max_depth and the criterion parameter. How does this change the results? Can you get better validation results then above?

Random forests (a bunch of random trees)#

The decisions made in the decision tree process are usually stochastic. If you look at the DecisionTreeRegressor, you’ll see there’s also an argument random_state to control it’s outputs.

We can take advantage of this randomness to fit an ensemble of many similar decision trees, then report the average and standard deviation of that ensemble to estimate uncertainty in the model predictions. This type of model is called a random forest. The same idea holds with many other stochastic models, but is particularly popular for decision trees.

from sklearn.metrics import mean_absolute_error, mean_squared_error
from sklearn.ensemble import RandomForestRegressor

model = RandomForestRegressor(n_estimators=90,max_depth=26)

# model has a fit function like every other supervised method in sklearn
model.fit(
    X=df_train["wavenumber [cm^-1]"].values.reshape((-1, 1)),
    y=df_train["absorbance"].values.reshape((-1, 1)),
)

val_MAE = mean_absolute_error(
    df_val["absorbance"].values.reshape((-1, 1)),
    model.predict(df_val["wavenumber [cm^-1]"].values.reshape((-1, 1))),
)
print(f"The MAE for the default decision tree regressor is {val_MAE:0.4f}")

The MAE for the default decision tree regressor is 0.0187

/tmp/ipykernel_2073/300074852.py:7: DataConversionWarning:

A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples,), for example using ravel().

Note the validation MAE here is a bit better than a single decision tree. This is a common pattern in machine learning and a technique that can be used to improve predictive power - fit an ensemble many identical models with different random initializations and average the predictions.

import numpy as np
import plotly.graph_objects as go

# Plot with plotly!
fig = go.Figure()
fig.add_scatter(
    x=df["wavenumber [cm^-1]"], y=df["absorbance"], name="Actual spectra data"
)
fig.add_scatter(
    x=df_train["wavenumber [cm^-1]"],
    y=df_train["absorbance"],
    name="Train data",
    mode="markers",
)
X_eval = np.arange(250, 4000, 0.1)
fig.add_scatter(
    x=X_eval,
    y=model.predict(X_eval.reshape((-1, 1))).reshape(
        (-1)
    ),  # Some tricks to make sure this is a vector
    name="Decision Tree Regressor spectra",
    line_color="#ff0000",
)
fig.add_scatter(
    x=df_val["wavenumber [cm^-1]"],
    y=df_val["absorbance"],
    name="Validation spectra",
    mode="markers",
)
fig.update_xaxes(title_text="Wavenumber [cm^-1]")
fig.update_yaxes(title_text="Absorbence [AU]")
fig.show()

Practice#

Try varying the n_estimators and max_depth parameters. How does this change the results? Can you get better validation results then above?

Gaussian process regression#

Gaussian processes are one of my favorite model types because they have many nice properties

They are exact (no fitting required)
They provide uncertainty estimates
They let you control how data is related
They make you think about what it means to be similar in the feature space
They are (usually) fast
They extrapolate in a controllable way
They are Bayesian and allow you to encode a prior belief

We could spend a whole semester talking about these models, but we’ll just cover the high-level choices here. Gaussian processes model predictions as an infinite ensemble of possible Bayesian predictions The most important design decision in a GP model is the covariance function that says how related two hypothetical data points for. The most popular function is the RBF or squared-exponential kernel

\[\begin{align*} k(x_i, x_j) = \exp\left(- \frac{d(x_i, x_j)^2}{2l^2} \right) \end{align*}\]

where \(x_i,x_j\) are feature vectors representing two possible data points, \(d(x_i, x_j)\) is the euclidean distance between the two vectors, \(l\) is a length scale that can be tuned, and \(k(x_1,x_2)\) is the covariance between the two points. Note that this function is basically saying far away points are uncorrelated, and close points are correlated (where “close” is >> or << \(l\)).

A GP predicts values by first:

Calculating a square matrix \(K(X,X)\) for all of the pairwise comparisons in the training dataset \(X\) using \(k(x_i, x_j)\)
Calculating a matrix \(K(X*,X)\) for how all of the desired datapoints (with features X*) are related to the dataset

After, it’s just a bit of linear algebra.

\[\begin{align*} \hat{\vec{y}}=K(X*,X)K(X,X)^{-1}\vec{y} \end{align*}\]

Numerical Methods and ML for ChE (F22-06-325)

Non-parametric models

Contents

Non-parametric models#

Example dataset - IR spectra#

Train/Val/Test split (given every 10th spectra, predict the rest)#

K-Nearest Neighbors#

Practice#

Decision Trees#

Visualizing decision trees#

Practice#

Random forests (a bunch of random trees)#

Practice#

Gaussian process regression#